Lãi suất là một trong những khái niệm cơ bản về tài chính mà các bạn học sinh được tiếp xúc từ sớm. Hiểu về cách tính lãi suất là 1 trong những bài học quan trọng không chỉ cho các kỳ thi trên lớp, mà còn là bài học quan trọng cho sự cân bằng và tự chủ tài chính trong tương lai.
1. Trước hết, lãi suất là gì?
Lãi suất là một từ ngữ khá lạ, “lãi” là một từ thuần việt kết hợp với một từ hán việt là “suất” để chỉ một nghĩa được thiết lập bởi một từ hán việt khác là “lợi suất”. Tuy nhiên, bài viết này chúng ta sẽ không bàn về nguồn gốc của từ ngữ, mà sẽ tìm hiểu về khái niệm lãi suất, các cách tính lãi suất thông dụng và hiểu về 1 sản phẩm tài chính có thể giúp cuộc sống bạn dễ thở hơn hoặc ngập đầu trong nợ nần nếu không biết cách sử dụng.
Lãi suất là một phần lợi được cộng thêm vào phần tiền gốc mà bạn hoặc phải trả nếu đi vay hoặc được nhận về nếu là tiền gửi tiết kiệm. Hãy tưởng tượng, bạn gửi toàn bộ tiền lì xì dịp tết khoảng 100 triệu, gửi vào ngân hàng, với lãi suất tiền gửi giả sử là 5%/năm, tức là sang năm sau, bạn có 5 triệu tiền tiêu vặt, sang năm kế tiếp cũng như vậy, bạn có thêm 5 triệu từ số tiền gửi ban đầu. Đây là cách tính lãi thông thường và đơn giản nhất.
Trước khi sang phần kế tiếp, WhySchools xin tổng hợp một số giải thích từ ngữ được sử dụng trong bài viết:
- Chu kỳ tính lãi: là khoảng thời gian mà ngân hàng hoặc tổ chức tài chính dùng để tính toán lãi suất cho khoản tiền gửi hoặc cho vay. Nó có thể là hàng ngày, hàng tháng, hàng quý, hoặc hàng năm, tùy thuộc vào điều khoản cụ thể của sản phẩm tài chính.
- Lãi suất: là tỷ lệ phần trăm mà ngân hàng hoặc tổ chức tài chính tính trên số tiền vay hoặc trả thêm cho số tiền gửi. Nó là chi phí của việc vay tiền (thứ bạn phải trả) hoặc lợi nhuận từ việc gửi tiền (thứ bạn kiếm được). Lãi suất có thể thay đổi tùy theo loại khoản vay hoặc tài khoản tiết kiệm, cũng như chính sách của ngân hàng.
- Vốn gốc: là số tiền ban đầu mà bạn vay hoặc gửi vào tài khoản. Đối với một khoản vay, vốn gốc là số tiền bạn mượn từ ngân hàng hoặc tổ chức tài chính. Đối với tài khoản tiết kiệm, vốn gốc là số tiền bạn đã gửi vào ngân hàng.
- Tiền lãi: là số tiền mà một người hoặc tổ chức phải trả thêm khi vay tiền hoặc nhận được khi gửi tiền. Lãi là phần thưởng cho người cho vay vì họ đã cho người khác sử dụng tiền của họ trong một khoảng thời gian nhất định.
1. Lãi suất thường và lãi suất kép khác nhau thế nào?
b. Lãi suất thường (simple interest) là gì?
“Vốn gốc để tính lãi suất thường có thể được xem như một miếng gỗ, vì nó trước sau như một”.
WhySchools xin lỗi vì câu đùa vô nghĩa vừa rồi. Tuy nhiên, cách tính lãi suất thường dựa trên sự cố định của tiền vốn gốc. Nghĩa là, nếu tính theo lãi suất thường, nếu như không có bất kỳ một biến động nào thì tiền vốn gốc luôn luôn được cố định. Cách tính lãi suất thường cũng khá đơn giản:
\text{Lãi} = \text{Tiền Gốc} \times \text{Lãi Suất} \times \text{Thời Gian}Sản phẩm tài chính thường sử dụng cách tính lãi suất đơn giản này đa phần là các dịch vụ tiền gửi tiết kiệm, vì nó khá có lợi cho ngân hàng trong việc dự trữ lượng tiền mặt và dùng cho việc rủi ro hơn và có khả năng sinh lợi cao hơn cho ngân hàng đó là các dịch vụ liên quan đến cho vay hoặc tín dụng. Và người dùng chúng ta được lợi thông qua tiền lãi mà hệ thống ngân hàng trả theo kỳ hạn thiết lập theo hợp đồng tiền gửi.
b. Lãi kép (compound interest) là gì?
Khác với lãi thường, lãi suất kép (compound interest) sẽ nhìn rất rắc rối trong mắt các bạn học sinh nếu như chỉ nhìn vào công thức, nhưng nếu biểu diễn thành đồ thị, và hiểu được bản chất vấn đề, công thức lãi kép sẽ dễ hiểu hơn hẳn.
Lãi kép có thể được hiểu một cách đơn giản là cộng phần tiền lãi vào vốn gốc để tính tiền lãi trong chu kỳ kế tiếp.
Giả sử chúng ta đã vay một khoản tiền 100.000 đồng từ ngân hàng WhySchools và với lãi suất kép hàng tháng là 10%, dưới đây chính là mô hình tính lãi theo hàng tháng cho đến khi chúng ta hoàn thành việc trả nợ:
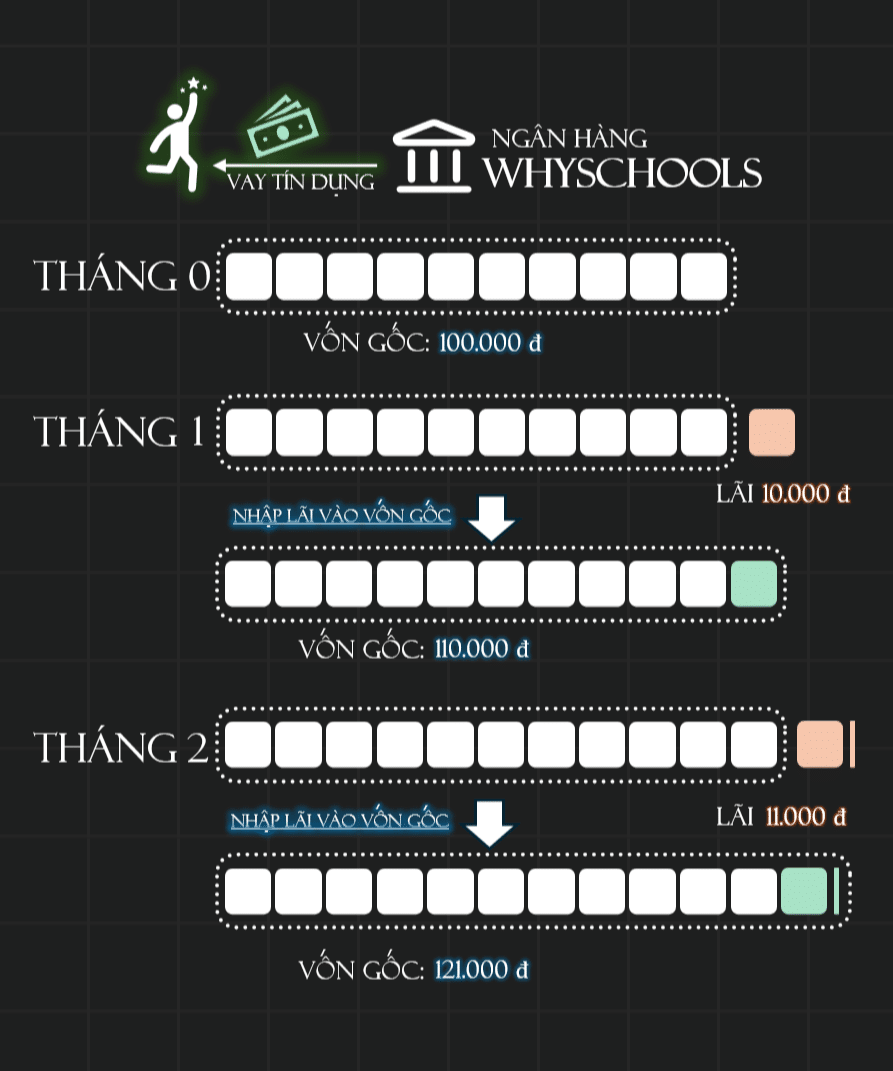
Lấy tháng 0 là mốc đầu tiên khi chúng ta bắt đầu vay tiền từ ngân hàng WhySchools, từ đó có thể tính được tiền lãi phải trả và biết được vốn gốc mà ngân hàng tính cho tháng tiếp theo theo quá trình sau:
- Tháng 1:
- Vốn gốc ban đầu (P1): 100.000 đồng (số tiền bạn Lan vay từ đầu)
- Lãi tháng 1 (L1): 100.000 x 0,10 = 10.000 đồng (tiền lãi của tháng đầu tiên)
- Tổng sau tháng 1 (A1): 100.000 + 10.000 = 110.000 đồng (tổng số tiền sau khi cộng lãi vào vốn gốc)
- Tháng 2:
- Vốn gốc đầu tháng 2 (P2): 110.000 đồng (số tiền sau tháng 1)
- Lãi tháng 2 (L2): 110.000 x 0,10 = 11.000 đồng (tiền lãi của tháng thứ hai)
- Tổng sau tháng 2 (A2): 110.000 + 11.000 = 121.000 đồng (tổng số tiền sau khi cộng lãi vào vốn gốc)
c. Diễn dịch thành công thức tính lãi kép (compound interest) cơ bản
Quá trình trên là một quá trình tính lãi kép khi vay được đơn giản hóa bỏ qua khá nhiều nghiệp vụ ngân hàng phức tạp, chu kỳ tính lãi thông thường của ngân hàng sẽ phụ thuộc vào hợp đồng cho vay hoặc hợp đồng tiền gửi, có thể theo hàng tháng, hàng quý hoặc hàng năm.
3. Dễ dàng chinh phục các bài tập về lãi kép
Nếu bạn không có khả năng nhớ công thức lãi kép hãy nhớ nguyên tắc sau:
Sau 1 chu kỳ, tiền lãi sinh ra được cộng vào tiền gốc để tính lãi cho chu kỳ kế tiếp.
Bạn đã hiểu về lãi kép chưa?
4. Một số sự thật thú vị về lãi suất và dịch vụ ngân hàng mà trường học không bao giờ dạy chúng ta:
Có một sự thật thú vị khi WhySchools tiếp xúc với các bài toán về lãi kép của khối THCS đó là: các bài toán về lãi kép thường gắn liền với việc gửi tiền tiết kiệm. Tuy nhiên, rất hiếm các dịch vụ tiền gửi tiết kiệm từ ngân hàng sử dụng lãi kép, hoặc nếu sử dụng nó sẽ được tách riêng thành một dịch vụ khác với tên gọi là dịch vụ đáo hạn, sau kỳ hạn bạn sẽ phải sử dụng dịch vụ đáo hạn để cộng lãi vào vốn gốc và tiếp tục chu kỳ tiền gửi mới.
Cách tính lãi kép thông thường được sử dụng với các sản phẩm thuộc về dịch vụ tín dụng và cho vay. Đồng thời chu kỳ tính lãi của các sản phẩm tín dụng hoặc cho vay thường ngắn hơn chu kỳ của tiền gửi tiết kiệm.
Với thực tế cuộc sống như thế, việc hiểu các bài toán về lãi kép không chỉ giúp các học sinh vượt qua các bài kiểm tra thường thấy trong lớp, mà còn là một bước đầu tiên giúp các bạn chuẩn bị cho một tương lai tài chính vững vàng. Hiểu rõ bản chất của các sản phẩm tài chính từ ngân hàng sẽ giúp các bạn học sinh không vướng vào những khoản nợ tiêu dùng bất tận, hoặc không được cho vay vì uy tín tín dụng thấp
Tài liệu tham khảo
WhySchools
